Breaking down “A monad is just a monoid in the category of endofunctors”

March 2019

“…just a monoid…”

Associativity is a property of some binary operations where the order of operations does not matter, e.g. since addition is associative,(a + b) + c = a + (b + c)

A finitary operation is an operation with finite arity

An algebraic structure is a set A together with a collection of finitary operations on A

A semigroup is an algebraic structure with a single associative binary operation.

An identity element is an element of a set that leaves other elements unchanged when combined with them (with respect to some binary operation).

A monoid is a semigroup with an identity element

∴ monoids make sense

“…in the category…”

A morphism is a mapping from some source object A to some target object B

An identity morphism is a morphism such that the source and target objects are the same object

A category is a collection of objects linked by morphisms, where the morphisms are such that they are associative and there exists an identity morphism for each object

∴ categories make sense

“…of endofunctors”

A functor F is a structure-preserving map between categories. That is, given two categories C and D:

• it associates each object X in c to an object F(X) in D
• it associates each morphism g: X → Y in C to a morphism F(g): F(X) → F(Y) in D such that

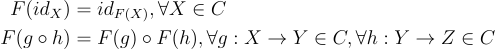
An endofunctor is a functor that maps a category to the same category

∴ endofunctors make sense

So what’s a monad?

…I’ve got no idea.